Author GU Jicheng
SUMMARY
In order to quantitatively describe the seismicity within certain area and period, a new mathematical quantity S , as a quantitative description of seismic activity, is introduced based upon the concepts of fuzzy entropy and weighted Hanuning distance of a fuzzy set in fuzzy mathematics. The following control factors are taken account of in 5: seismic frequency, average magnitude or average energy release, maximum magnitude, and the concentration of special distribution of the events as well as its time memory effect.
Key words: seismic activity, seismicity, application of fuzzy mathematics.
INTRODUCTION
An important, perhaps the most frequently used technical term in seismology is seismicity or seismic activity, by means of which seismologists attempt to describe the seismic frequency of earthquakes, even risk and hazard and so on in an investigated region. And therefore seismicity plays a very important role in earthquake prediction.
In last two decades, the concepts of “seismic gap” and “guiescence” as a kind of special seismic phenomena have been described.
The concepts, however, are unclear, vague. There is no quantitative description. For example, what means “The seismic activity in this area is high (or low)” How high means high? There is no standards, no scale.
In order to quantitatively describe seismic activity, some authors have worked on this problem in the view point of seismology (U.b.Riznichinko, 1958, Wu Ja-yi, 1983), statistics (Shozo Matsumura 1984), and even fuzzy mathematics (Peek R., J.B.Berrill and R.O.Dvis, 1980). Because certain reasons these formulas are not widely accepted by seismologists yet. Since Zadeh (1965) first developed the concept of fuzzy mathematics, the literature on fuzzy theory and its applications have grown rapidly.
As an application of fuzzy mathematics to seismology hereby are proposes this new quantity S to be a comprehensive quantitative description of seismic activity.
SEISMICITY S
1. Definition
Let A be a fuzzy subset of the universe of discourse of seismic activity
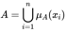
(1)
where μA(xi) (i=1, 2, ……n) are the membership functions. According to the understanding of seismology, x should be the seismic frequency N, average magnitude m or average energy release, maximum magnitude M, average distance among the epicenters respectively and correspond to the measurements of tempral, energy and spatial factors. And therefore one denote the membership functions as μA(N), μA(m̅), μA (M) and μA (d).
On the other hand,one defines a special subset A, which belongs to the universe of discourse and represents the case of complete quiescence, and have
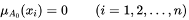
Actually,
Actually one can see that set A0 is an ordinary set.
According to the concept of the weighted Hamming distance between eubsets A and A0, the seismicity function S corresponding to the fuzzy subset A is defined by
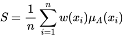
(3)
where w(xi) (i=1, 2, ….n) are weight factors. Once the membership function μA(xi)and weight factors w(xi) (i=1, 2, ….n) are given, the seismicity function S can be obtained immediately from eq. (3).
2. Membership function
Now let us didscuss the membership functions in eq. (3) basad upon the seismological consideration.
(1)Membership function of seismic frequency μA(N)
It is usual that within certain area and period,the larger the seismic frequency N, the more active the seismicity. Quiescence means N is or closes to zero. The format of the membership function μA(N) is taken as
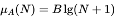
(4)
where B is a parameter (constant).
Because the number of events N depends on the control ability of a network, sensitivity of instrument, and on the recording conditions, in other works, N depends on the lower limitation of magitude, the following lower limitation is suggested:

(5)
Now looking back on parameter B. B is chosen to meet the following equation
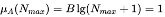
(6)
where N is the possible maximum value of N. According to the real seismological situation, e.g. Xing Tai earthquake of 1966 in North China(M=6.8) there were 110 events of M≥3 only during the first day after the mainshock, and consider formulas (8) and (9), the value of B=0.25 is suggested and used in the calculation of this work. And so for Xing Tai earthquake mentioned above, μA(N)=0.511.
(2) Membership function of average magnitude,or of average energy release μA(m̅).
Besides seimic frequency N, magnitude is an other important index of seismicity. One makes use of the average magnitude m to describe the average energy release of each event.
According to Gutenberg-Richter formula:
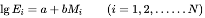
(7)
The average energey release is given by
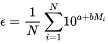
(8)
and therefore
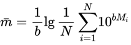
(9)
For the format of μA(m̅), the special case of the half trapezoid-distribution (He Zhong-Xiong, 1982) is used
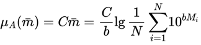
(10)
In order to insure the grade of membership function is 1 at maximum value of m̅ (assume the maximum m̅ (is 9.0), parameter C is chosen as C=0.11. So, if b=1.5.
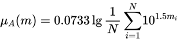
(11)
(3) Membership function of maximum magnitude μA(M).
The maximum magnitude M of a sequence is also one of the indexes of seismic activity.
Despite the maximum magnitude M has been used in the calculation of the average magnitude m̅, but the effect of M might not be completely involved yet. So one choose the same format of the membership function of μA(M) as that of μA(m̅), i.e.
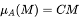
(12)
(4) Membership function of the density of spatial distribution of earthquakes μA(d).
Finally, one discusses the spatial factor of seismicity. Usually if the epicenters of earthquake distribute densily, seismologists consider that the seismic activity in this area is active. Otherwise, quiet.
Hence, one introduces an average distance d to measure this distribution and d is determined by
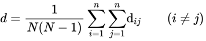
(13)
where dij is the distance between i-th epicenter of earthquake and j-th one.
dij can be given by

(14)
or
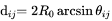
(15)
where R0 is the average radius of the Earth (R0=6,370km); (xi, yi) is the surface Cartesian coordinates of the i-th event, and ϕi, λi are the latitude and the longitude of an earthquake,
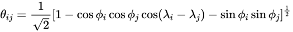
(16)
In order to construct the membership function, the following decreasing r-distribution (Ho Zhong-xiong 1982) is employed.
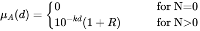
(17)
where k is a constant, and is chosen as k=0.01(km)^(-1), d is average distance(unit: km); and R is a memory effect factor and is given by
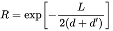
(18)
Finally, one discuss the weight factor of formula(3) W(x); An estimated and suggested value is that
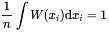
(19)

(20)
Accordingly, from formulas (3), (4), (10), (11), (17) and (20), one has
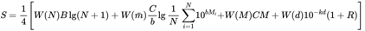
(21)
where b=1.5, the suggested values for other parameters are follows:
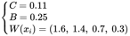
(22)
When the global seismicity Sg is considered, the fourth term in eg. (24) should be omitted.
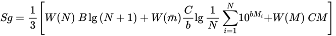
(23)
As an example, Fig.I shows the seismic activity S and its variation with time of Haicheng earthquake (M=7.3, Feb.4, 1975, China). The time interval to calculate S is 30 days. The lower limitation of earthquake Mc is 3.0. As seeing from this fig. that in the first mouth immediately after and including the main shock, S=0.613 then S decreases rapidly; about 200 days after the main shock, the first quiescence appears (S=0)……
DISCUSSION AND CONCLUSION
1. In order to quantitatively describe seismicity, a new quantity S is introduced based upon the concept of the weighted Euclidean distance between two fuzzy subsets which belong to the universe of discourse of seismic activity in certain tempral and special domain. S has contained the following factors: seismic frequency N, average energy release, maximum magnitude and density of spatial distribution of epicenters.
2. The suggested values of the parameters in S are chosen by physical considerations. They might be modified fater somemore practices.
3. As example to calculate S the seismie activity S and its variation with time for the sequence of Haicheng earthquake of 1975 in China (M=7.3) is given.
REFERENCES
Feng, Deyi, et al., Applications of fuzzy mathematics to earthquake prediction and investigation of the preparatory model of earthquake source, Northwestern Seism.J.,vol.13,1981(in Chinese)
Feng, Deyi, et al., The statistical indexes of seismicity and the probability prediction for time of earthquake occurence,J.of Seism.Res.vol.4,1981.(in Chinese)
Feng, Deyi, et al., Technique in fuzzy Mathematics and Its Applications, Seism.Pr., 1983(in Chinese)
He,Zhongxuong, Fuzzy mathematics and Its applications, 1982 (in Chinese)
Kandel,Abraham, fuzzy Techniques in Pattern Recognitiion, New York, Wiley, 1982.
Mamdani E.H. & Gaines, B.R.ed, Fuzzy Reasoncing and Its Applications. London, Academic Pr.1981).
Negoita, C.V. Fuzz Systems, Tunbride Wells, Abacus Pr., 1981.
Peek r,J.B. Berrill, R.O. Dvis, A seismicity model for New Zealand National Soc. For Earth.Eng.Vol.13,1984
Wang, Biquan. et al., Pattern recognition of seismicity before strong earthquakes. Acta Seism.Sinica.Vol.4, 105-115, 1982 (in Chinese)
Wang,Biquan & Ma, Xiufang, Applications of pattern recognition to the study of the dynamic factor of occurence of large earth-quakes. Acta Seism. Sinica, vol.5, 257-267, 1983 (in Chinese)
Wu, Jayi&gao, Xue-Feng, On the problem of quantization of seismicity Earthquake, 5 1983 (in Chinese)
[Click below for the whole paper]

Jicheng GU initially defined seismicity in 1985. This paper describes a new mathematical quantity of Seismic Activity (Seismicity) S.